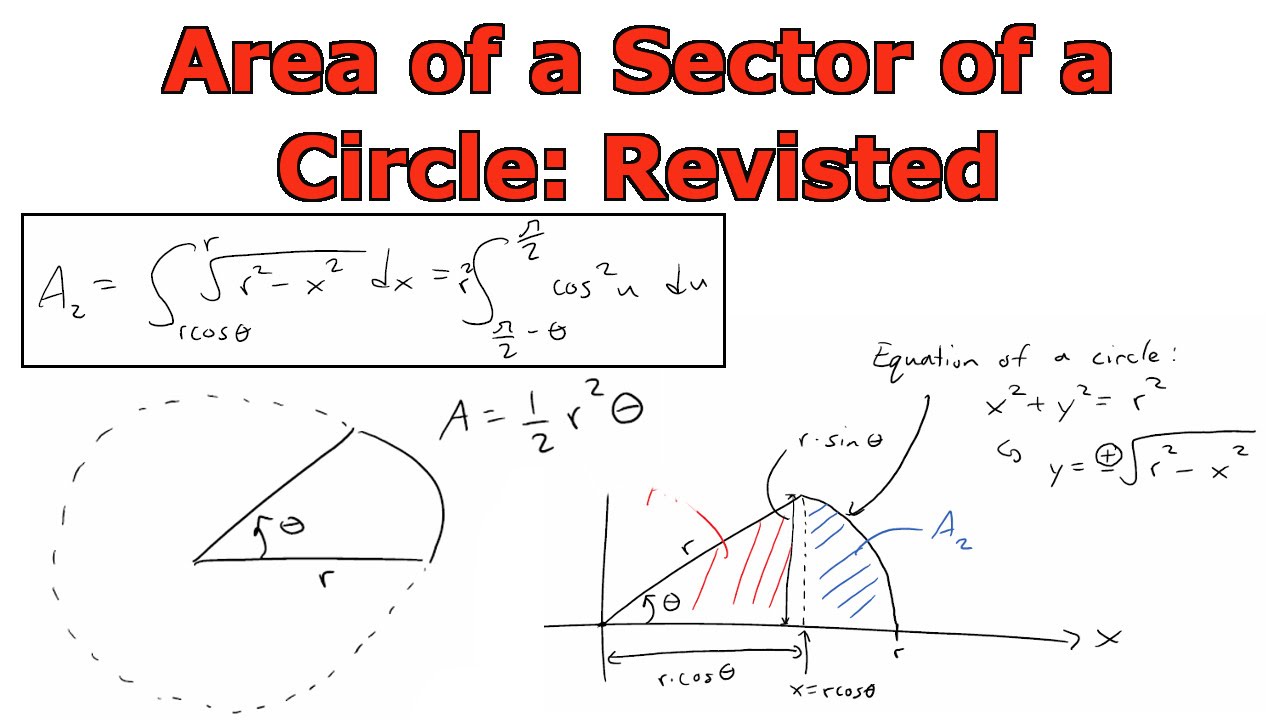
Area and Perimeter of the Circle Formula and Derivations

duaism.best

Using Definite Integration To Find Area Of A Circle With

For example, the 'normal' integrals you are talking about are really a special case of line integral through a one-dimensional scalar field, special in the sense that the parametric curve through the field is a straight line (as another aside you can parameterise your 'normal' integral w.r.t. dx to one w.r.t dt and integrate 'backwards' like how Khan showed a few videos ago using the a + b - t.

How To Calculate Area Of Circle Using Integration Haiper

Nov 8, 2003. Circle Integral. In summary, the integral sign with a circle on it usually refers to a line integral, which is the integral of a function around a closed loop in the domain of the function. It can also be extended to higher dimensions. A line integral is performed over a one-dimensional subspace of the domain, while a "normal.

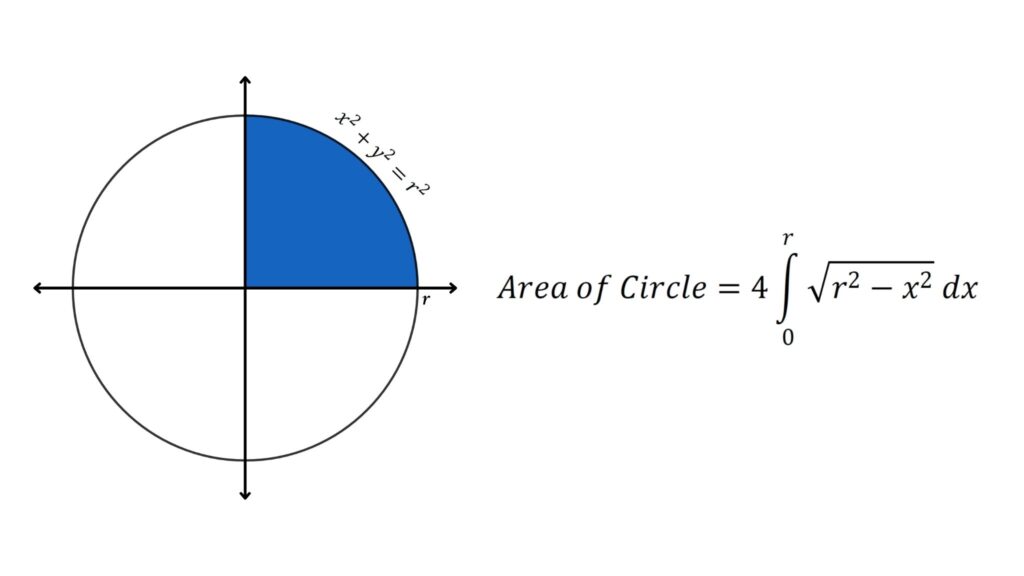
Area and Perimeter of the Circle Formula and Derivations

I know from multivariable calculus that the integral sign with circle in its middle means integrating along a closed path. So when I encountered in complex analysis the above integral sign but with an arrow on the circle to indicate orientation, I automatically assumed oriented closed contour.. But now on reading my textbook carefully, it only says that the arrowed circle actually means.

integration Line Integral of a circle Mathematics Stack Exchange

In mathematics, an integral is the continuous analog of a sum, which is used to calculate areas, volumes, and their generalizations.Integration, the process of computing an integral, is one of the two fundamental operations of calculus, the other being differentiation.Integration was initially used to solve problems in mathematics and physics, such as finding the area under a curve, or.

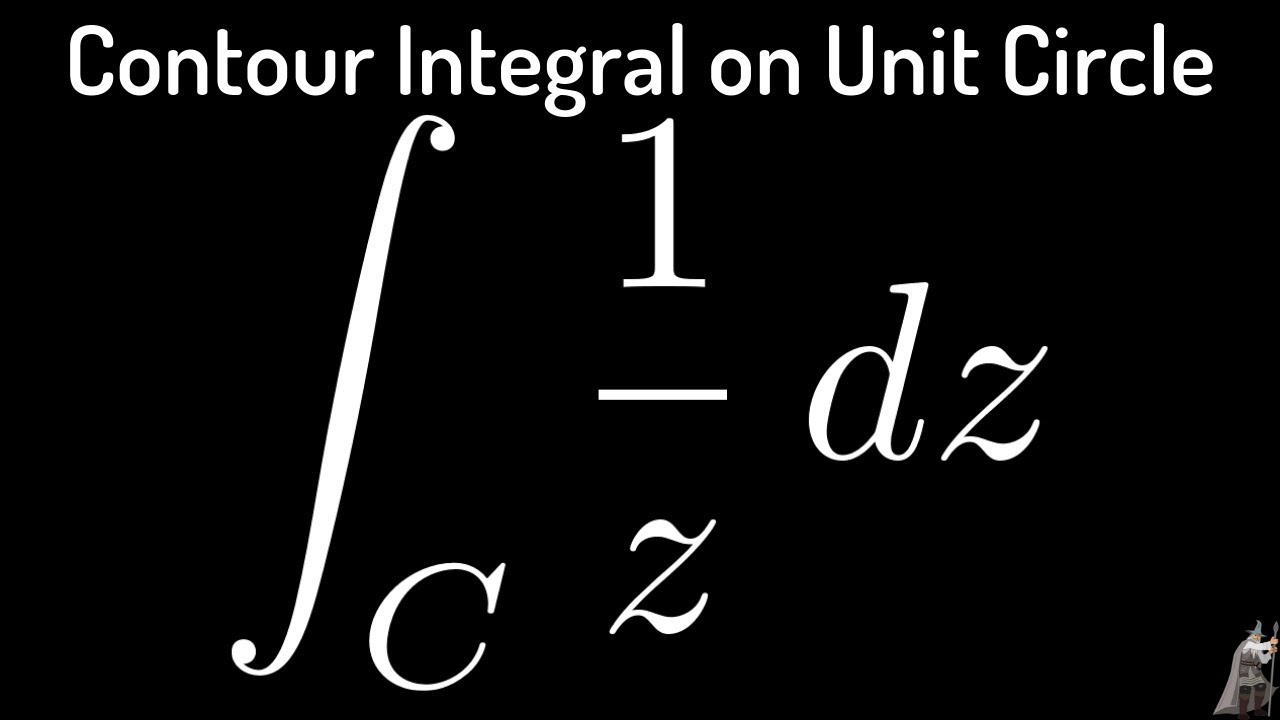
Contour Integral of 1/z with respect to z along the Unit Circle Complex Variables YouTube

Introduction to Integration. Integration is a way of adding slices to find the whole. Integration can be used to find areas, volumes, central points and many useful things. But it is easiest to start with finding the area between a function and the x-axis like this:

Integration round the unit circleMethod of contour integrationPart 1Theta Classes YouTube

The ∫ Symbol in Mathematics: Integral. The realm of mathematics is teeming with symbols that encapsulate deep and intricate concepts. One of the most recognizable and foundational symbols is the ∫ symbol, denoting the concept of integration. This article will delve into its meaning, core applications, and offer some illustrative examples. Usage

Area of circle using integration

But this is the (implicit) equation for a circle — the extra condition that \(y\geq0\) makes it the equation for the semi-circle centerd at the origin with radius 1 lying on and above the \(x\)-axis. Thus the integral represents the area of the quarter circle of radius \(1\text{,}\) as shown in the figure on the right below. So

Definite Integral Calculate, Formula, Properties

It's an integral over a closed contour (which is topologically a circle). 0 0 0. It basically means you are integrating things over a loop. For e.g. a circle with an element dl d l if you do ∮dl ∮ d l it will give you circumference of the circle.

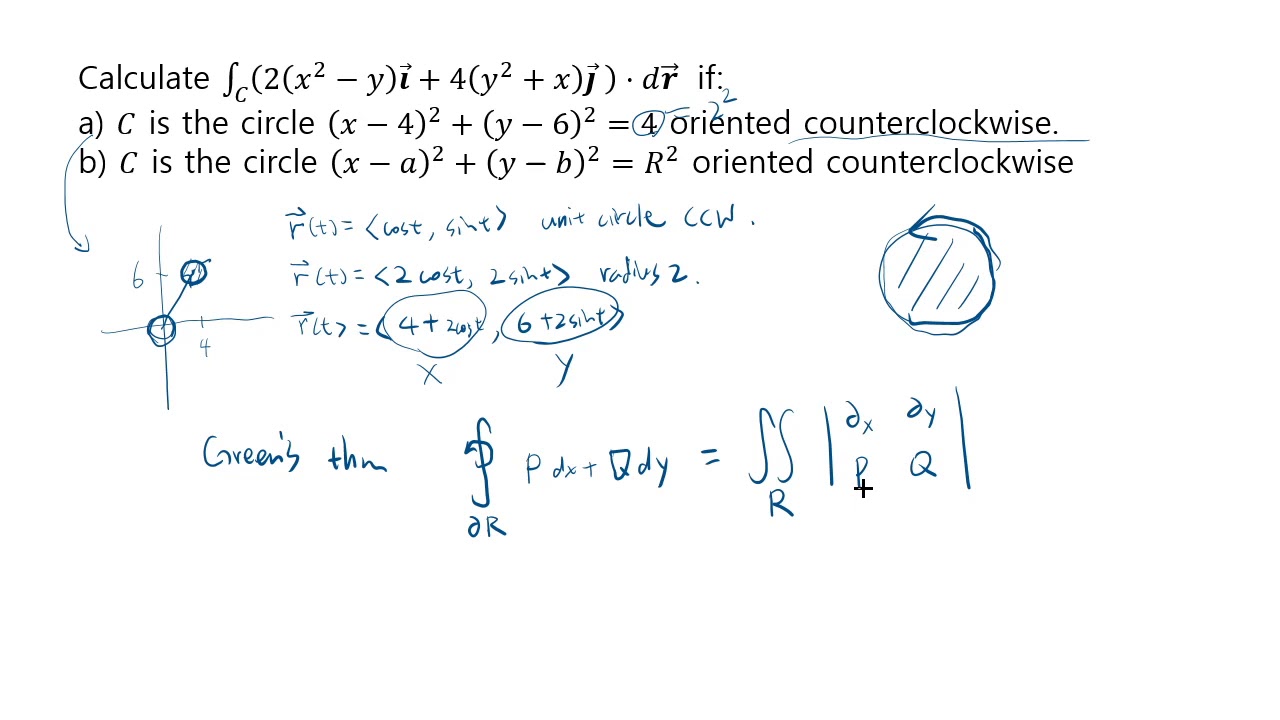
line integral going around a circle centered at some point YouTube

the integral giving L = Z dℓ = a Z 2π 0 dθ = aθ |2π 0 = 2πa , as expected. Now let's ﬁnd the area of the same circle. It is pos-sible to ﬁnd areas by performing multiple integrals, but since many physics students have not seen these before, we will ﬁnd areas by cleverly cutting the shape whose area is to be found into strips of.

What is an integral? + Example

Definite Integrals. The red area is above the axis and is positive. The blue area is below the axis and is negative. A definite integral is a formal calculation of area beneath a function, using infinitesimal slivers or stripes of the region. Integrals may represent the (signed) area of a region, the accumulated value of a function changing.

Evaluate Definite Integral using Limit Definition with Riemann Sums YouTube

Meaning Unicode LaTeX;. While the English integral symbol leans to the right, the German symbol (used throughout Central Europe) is upright, and the Russian variant leans slightly to the left to occupy less horizontal space. Another difference is in the placement of limits for definite integrals. Generally, in English-language books, limits.

Closed circle integral of 1/z and branch cuts YouTube

This is called a double integral. You can compute this same volume by changing the order of integration: ∫ x 1 x 2 ( ∫ y 1 y 2 f ( x, y) d y) ⏞ This is a function of x d x. ‍. The computation will look and feel very different, but it still gives the same result.

The Mean Value Theorem For Integrals Average Value of a Function YouTube

The integral symbol ∫ is used to represent integration in calculus. Typically, the integral symbol is used in an expression like the one below. ∫ ab f (x)dx. In plain language, this means take the integral of the function f (x) with respect to the variable x from a to b. See integral notation for typesetting and more.

Line Integral over right half of a circle YouTube

In calculus and analysis, constants and variables are often reserved for key mathematical numbers and arbitrarily small quantities. The following table documents some of the most notable symbols in these categories — along with each symbol's example and meaning. π. If f ( x) → L, then f ( x) 2 → L 2.

How To Calculate Area Of Circle Using Integration Haiper

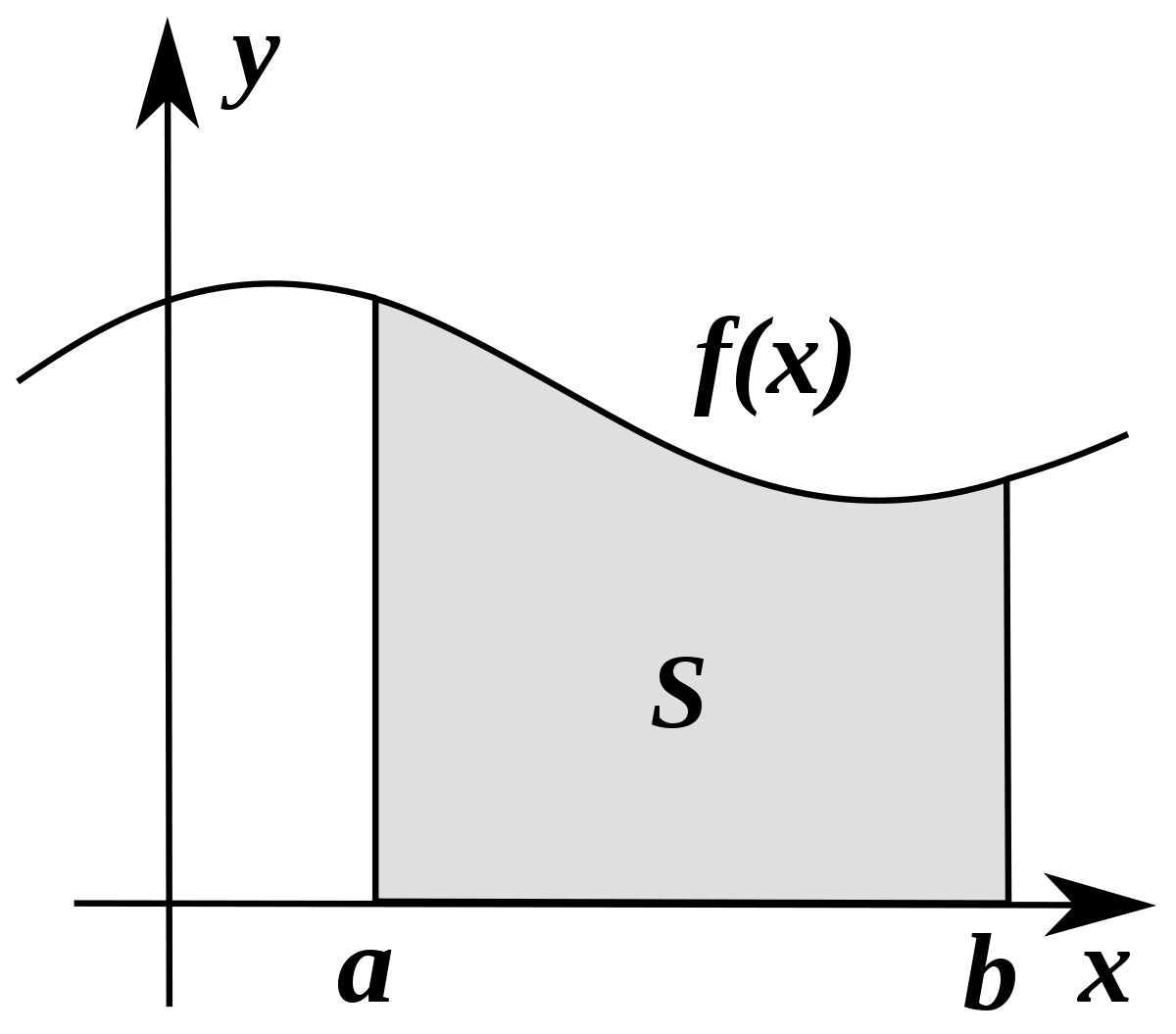
The definite integral of a function f over an interval [a,b] represents the area defined by the function and the x-axis from point a to point b, as seen below. The symbol used to represent this area S and integral, respectively, is. S = ∫ b a f (x)dx, where. You might be wondering what dx means.

Finding Area of a Circle using Calculus_Part I Using Rectangular (i.e. Cartesian) Coordinates

integral, in mathematics, either a numerical value equal to the area under the graph of a function for some interval (definite integral) or a new function the derivative of which is the original function (indefinite integral). These two meanings are related by the fact that a definite integral of any function that can be integrated can be found.